2次密度行列の直接決定法

分子の基礎的な物性を表現する演算子は、一体もしくは二体の演算子です。 ゆえに、分子のそうした物性は、正確な2次密度行列が与えられればすべて計算できます。 2次密度行列は、高々4電子の座標にのみ依存する量ですから、 N電子の座標に依存する波動関数の代わりに、2次密度行列を用いて、 量子力学を再構築することができれば、非常にシンプルな表現が得られる可能性があります。

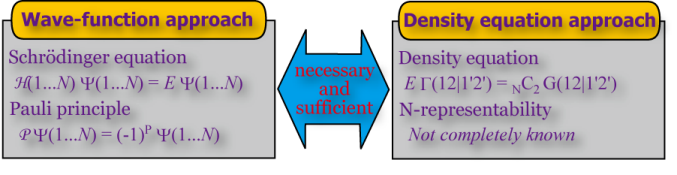
中辻は、1976年にその基礎となる密度方程式(Density equation)を提案しました。 （密度方程式は後に、欧米の研究者の間でcontracted Schrödinger equationと呼ばれています） 密度方程式は、密度行列の世界で表現された、Schrödinger方程式に等価な方程式です。 1996年に、中辻と安田は、Valdemoroの理論を改良し、現実の分子について密度方程式を解くことに、 世界で初めて成功しました。2001年には、中辻と中田らは、 半正定値計画問題を2次密度行列の直接決定法に適用し、 密度行列の変分法とその分子系への応用を発表しています。 この方法は、多参照の波動関数が必要となる系や、強電子相関系にも有効であることが示されています。