?
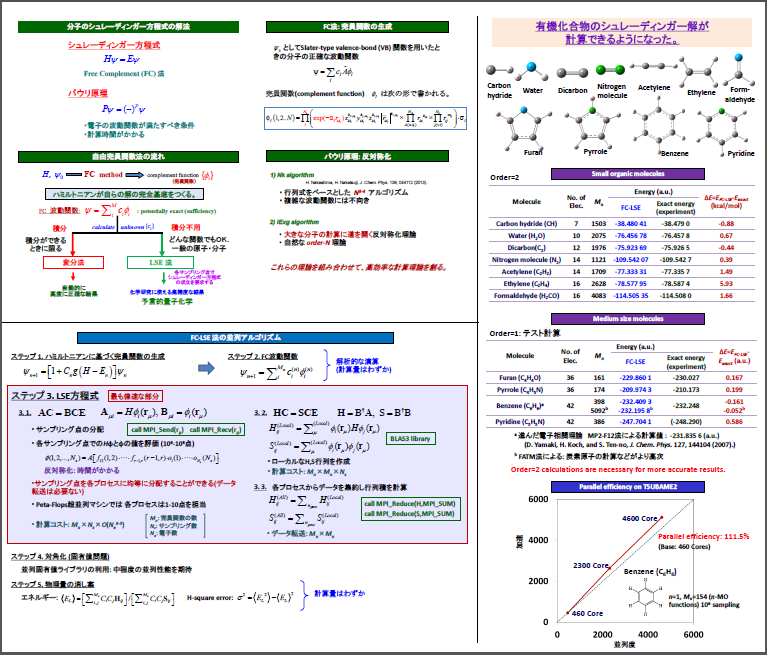
シュレーディンガー方程式は化学の世界を支配する方程式とされ、これを正確に解く方法を確立することは多くの理論研究者の夢であった。しかし、その夢はシュレーディンガー方程式の発見以来80年にわたって実現されなかった。しかし、最近中辻によってその一般的な解法が発見された。彼が発見したいくつかの方法の中で最もよく使われているのは自由完員関数(FC)法である。この方法を使うと正確な波動関数を張る「完員」関数が系のハミルトニアンを使って自動的に生成されるので、その展開係数ci を計算すればシュレーディンガー方程式の解が得られる。その方法としては変分法とlocal Schroedinger equation (LSE)法がある。後者は分子中の各座標でシュレーディンガー方程式が成立している事を条件式としてこの係数を求める方法であり、完員関数の積分法が確立されていなくても使える利点がある。
?このように、FC法は自動的にシュレーディンガー方程式を解く一般的な方法であり、夢の方法と言って良い。「ハミルトニアンは系のあらゆる情報を含み、これが正確な解を記述する「完員」関数をFC法によって自動的に生成する。」この様に、この方法は対象ごとに最適の関数を作る完備な方法である。
この方法を科学と化学の広範な対象に応用できるようにすることは、次の大きな研究対象であり、量子科学研究協会研究所で鋭意進められている。
東工大TSUBAMEグランドチャレンジ(2013年春・秋)に採用され、その結果がSC13(米国デンバー)にて発表されました。
この方法を用いて原子・分子のシュレーディンガー方程式を解くプロジェクトが、東京工業大学のTSUBAMEグランドチャレンジ課題(2013年春季・秋季)に審査のうえで採用されました。その成果は2013年11月17日?22日に米国デンバーで開催されたSC13にて発表されました。
References
- Discovery of a General Method of Solving the Schrödinger and Dirac Equations That Opens a Way to Accurately Predictive Quantum Chemistry, H. Nakatsuji, Acc. Chem. Res., 45, 1480-1490 (2012). This article is ranked 4 in Most Read Articles in July 2012
- Scaled Schrödinger Equation and the Exact Wave Function, H. Nakatsuji, Phys. Rev. Lett. 93, 030403 (2004).
- General Method of Analytically Solving the Schrödinger Equation of Atoms and Molecules, H. Nakatsuji, Phys. Rev. A, 72, 062110 (2005).
- Deepening and Extending the Quantum Principles in Chemistry, H. Nakatsuji, Bull. Chem. Soc. Jpn. 78, 1705 (2005).
- Analytically Solving the Dirac-Coulomb Equation for Atoms and Molecules, H. Nakatsuji H. Nakashima, Phys. Rev. Lett., 95, 050407 (2005).
- Free ICI (Iterative Complements Interaction) Calculations of Hydrogen Molecule, Y. Kurokawa, H. Nakashima, and H. Nakatsuji, Phys. Rev. A, 72, 062502 (2005).
- Structure of the Exact Wave Function, H. Nakatsuji, J. Chem. Phys., 113, 2949-2956 (2000).
- Structure of the Exact Wave Function. II. Iterative Configuration Interaction Method, H. Nakatsuji and E. R. Davidson, J. Chem. Phys. 115, 2000-2006 (2001).
- Structure of the Exact Wave Function. III. Exponential Ansatz, H. Nakatsuji, J. Chem. Phys., 115, 2465-2475 (2001).
- Structure of the Exact Wave Function. IV. Excited Sates from Exponential Ansatz and Comparative Calculations by the Iterative Configuration Interaction and Extended Coupled Cluster Theories, H. Nakatsuji, J. Chem. Phys., 116, 1811-1824 (2002).
- Structure of the Exact Wave Function. V. Iterative Configuration Interaction Method for Molecular Systems within Finite Basis, H. Nakatsuji and M. Ehara, J. Chem. Phys., 117, 9-12 (2002).
- Iterative CI General Singles and Doubles (ICIGSD) Method for Calculating the Exact Wave Functions of the Ground and Excited States of Molecules, H. Nakatsuji, M. Ehara, J. Chem. Phys. 112, 194108 (2005).
- Inverse Schrödinger Equation and the Exact Wave Function, H. Nakatsuji, Phys. Rev. A 65, 052122 (2002).