Directly solving 2nd-order reduced density matrices without using wavefunctions
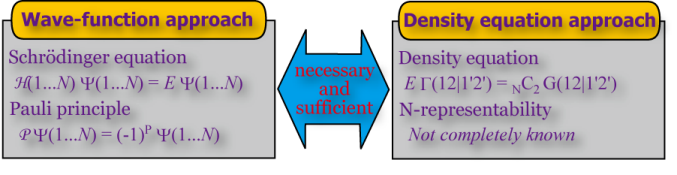
?? Since any basic operators of properties include only one- and two-electron operators, all the properties of molecules can be calculated if the exact second-order density matrices are given. The second-order density matrix depends only on 4 electron coordinates at maximum. Therefore, we may construct quantum mechanics using the second-order density matrix as a basic variable instead of the wave function (Wave Mechanics without Wave).
?? Nakatsuji presented in 1976 a basic equation called density equation (or later called contracted Schrödinger equation, again in the West World) which is equivalent to the Schrödinger equation in the space of the density-matrix. In 1996, by improving Valdemoro’s theory, Nakatsuji and Yasuda firstly solved the density equation for real molecules. In 2001, Nakatsuji and Nakata further invented a variational method for directly solving the second-order density matrices of molecules using positive semi-definite programming (SDP) algorithm. This method was further shown to be stable under the multi-reference and strong-correlation situations.
?

References
- Equation for the Direct Determination of the Density Matrix, H. Nakatsuji, Phys. Rev., A14, 41 (1976).
- Equation for the Direct Determination of the Density Matrix: Time- Dependent Density Equation and Perturbation Theory, H. Nakatsuji, Theor. Chem. Acc. 102, 97-104 (1999).
- Direct Determination of the Quantum-Mechanical Density Matrix Using the Density Equation, H. Nakatsuji and K. Yasuda, Phys. Rev. Lett., 76, 1039-1042 (1996).
- Direct Determination of the Quantum-Mechanical Density Matrix Using the Density Equation. II., K. Yasuda and H. Nakatsuji, Phys. Rev. A 56, 2648-2657 (1997).
- Density Equation Theory in Chemical Physics, H. Nakatsuji, in Many-electron Densities and Reduced Density Matrices, edited by J. Cioslowski, Kluwer Academic, New York 2000, pp85-116.
- Variational Calculations of Fermion Second-Order Reduced Density Matrices by Semi- definite Programming Algorithm, M. Nakata, H. Nakatsuji, M. Ehara, M. Fukuda, K. Nakata, and K. Fujisawa, J. Chem. Phys., 114, 8282-8292 (2001).
- Density Matrix Varitional Theory: Application to the Potential Energy Surfaces and Strongly Correlated Systems, M. Nakata, M. Ehara, and H. Nakatsuji, J. Chem. Phys., 116, 5432-5439 (2002).
